Biologie de conservation via Réintroduction / Renforcement
Description
Pour ce modèle, on s'intéresse à l'introduction d'invidus appartenant à une espèce absente, en voie de disparition, ou éteinte dans un milieu. Cela s'inscrit donc dans un contexte de biologie de la conservation : le but est d'atteindre un seuil confortable de population permettant son établissement. La densité étant très faible au début de l'opération, il faudra faire attention à un mécanisme affectant les populations de petite taille : l'effet Allee.
Fonctionnement du modèle
Deux types d'agents peuplent le modèle : les femelles et les mâles. Un pas de temps n'a pas de représentation réelle, il s'agit d'une unité arbitraire, qu'il faut calibrer en accord avec les autres paramètres temporels (espérance de vie, période de propagule, catastrophes, etc.). L'espace est continu et torique, c'est à dire que les bords sont connectés.
Les mâles parcourent des distances plus grandes (deux fois plus) que les femelles. A chaque pas de temps, un mâle se déplace, se reproduit avec une femelle aux alentours s'ils sont tous les deux matures et que cette dernière le choisit comme partenaire, puis peut mourir avec une certaine probabilité fixe. Les femelles sont les seules à pouvoir produire une descendance. A chaque pas de temps, une femelle se déplace, puis cherche à se reproduire si elle est mature. Dans ce cas, elle cherche un mâle également mature aux alentours, et s'accouple avec l'un d'entre eux au hasard avec une probabilité croissante du nombre de partenaires éligibles. S'il y a reproduction, le juvénile survit avec une probabilité décroissante du nombre de conspécifiques voisins. Enfin, la femelle peut mourir avec une certaine probabilité fixe. Cette implémentation du processus de reproduction sexuée fait qu'une densité de population plus forte augmente, pour chaque femelle, la probabilité d'engendrer une decendance. C'est le principe de densité dépendance positive, et on observe l'émergence d'un effet Allee fort pour ce modèle.
L'algorigramme suivant récapitule le fonctionnement du modèle :
Afficher l'algorigramme
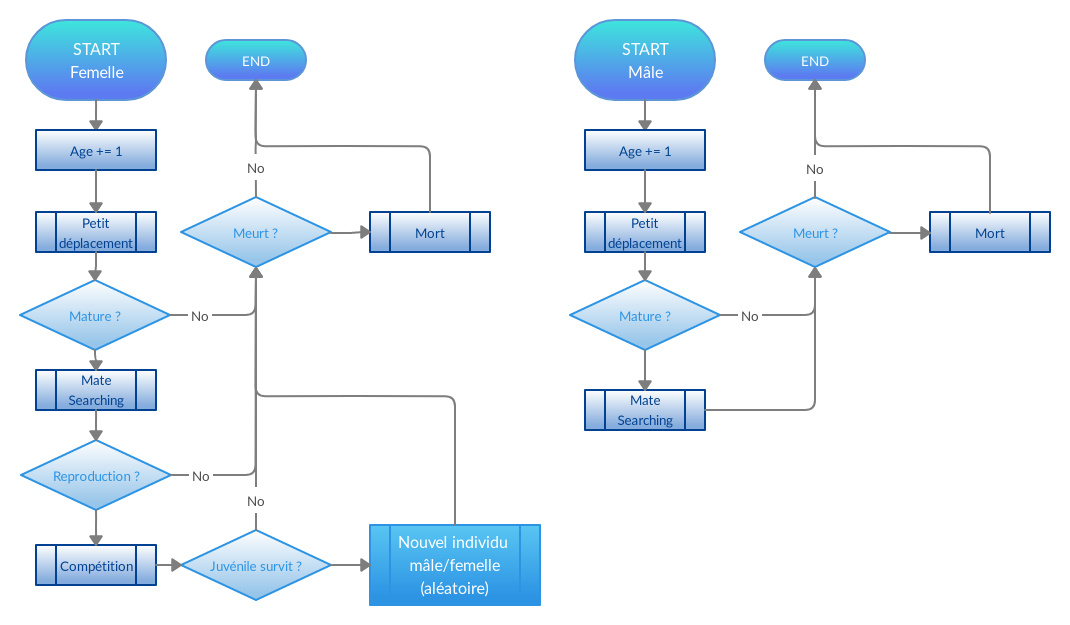
Résultats
Les résultats obtenus sont cohérents avec les attentes théoriques. Dans un contexte de biologie de la conservation, la pression de propagule, notamment via le taux d'introduction µ, est un facteur prépondérant de l'efficacité des introductions. Lorsque l'objectif est la rapidité d'établissement, les lâchers rares mais de grande taille sont à privilégier aux lâchers plus fréquents et plus petits, en raison de la densité dépendance positive qui favorise la coopération entre les individus. C'est également pour cette raison que regrouper les lâchers en un nombre réduits de points est une approche judicieuse. Attention toutefois à ne pas surencombrer les points de lâchers, auquel cas la compétition peut venir entraver l'opération.
Prendre en compte la variance dans le temps d'introduction comme second critère d'optimisation nuance aussi cette conclusion. La stratégie optimale stricte reste celle correspondant à un établissement dès le premier lâcher; mais dans l'incapacité de calibrer correctement l'introduction, ce qui est certainement le cas en pratique, cette stratégie peut se révéler à double tranchant : une taille et une fréquence de propagule légèrement différente peut grandement défavoriser le MFPT et le VFPT. Considérer des lâchers plus petits mais plus fréquents, qui ont une performance similaire entre eux, est un compromis tout à fait pertinent. Cette tendance est de plus en plus marquée selon que le taux d'introduction augmente.
En présence de catastrophes, on revient à une optimalité des lâchers de grande taille plus rares. La population doit s'établir entre deux occurrences de catastrophe, ce qui est le plus probable en partant d'une taille de propagule grande. Les lâchers plus fréquents sont à privilégiér seulement pour des taux d'introduction forts, avec des catastrophes plus clémentes sur la population.